Không chỉ xuất hiện trong công thức, gia tốc dao động điều hòa còn quyết định chiều chuyển động, vị trí cân bằng và mối liên hệ chặt chẽ với vận tốc, li độ. Bài viết dưới đây Trung tâm gia sư The TutorX sẽ giúp bạn nắm vững công thức, đồ thị và các dạng bài tập thường gặp về gia tốc trong dao động điều hòa.
Công thức gia tốc dao động điều hòa
Trong dao động điều hòa, vật chuyển động qua lại quanh vị trí cân bằng theo quy luật hình sin hoặc cos. Gia tốc của vật không đổi mà biến thiên theo thời gian và vị trí.
Công thức tổng quát của gia tốc dao động điều hòa
Gia tốc trong dao động điều hòa được xác định theo công thức:
a = –ω²x
Trong đó:
- a: gia tốc của vật (m/s²)
- ω: tần số góc (rad/s)
- x: li độ của vật so với vị trí cân bằng (m)
Dấu “–” cho thấy gia tốc luôn hướng về vị trí cân bằng, tức là gia tốc có chiều ngược với li độ.

Công thức gia tốc theo thời gian
Nếu phương trình dao động của vật là:
x = A cos(ωt + φ)
Thì gia tốc tương ứng sẽ là:
a = –ω²A cos(ωt + φ)
Điều này cho thấy:
- Gia tốc biến thiên điều hòa theo thời gian
- Gia tốc cùng pha với li độ, nhưng ngược chiều
Giá trị cực đại của gia tốc
Gia tốc đạt giá trị lớn nhất khi vật ở vị trí biên:
amax = ω²A
Xem thêm: Gia tốc có thể âm không?
So sánh gia tốc vận tốc và li độ trong dao động điều hòa
Để hiểu sâu về gia tốc dao động điều hòa, cần đặt nó trong mối quan hệ với vận tốc và li độ.
Mối quan hệ giữa gia tốc và li độ
- Gia tốc tỉ lệ thuận với độ lớn li độ
- Gia tốc ngược chiều với li độ
- Khi vật ở vị trí cân bằng (x = 0) ⇒ a = 0
- Khi vật ở vị trí biên (|x| = A) ⇒ |a| = amax
Mối quan hệ giữa gia tốc và vận tốc
- Khi vận tốc cực đại ⇒ gia tốc bằng 0
- Khi gia tốc cực đại ⇒ vận tốc bằng 0
- Gia tốc sớm pha π/2 so với vận tốc
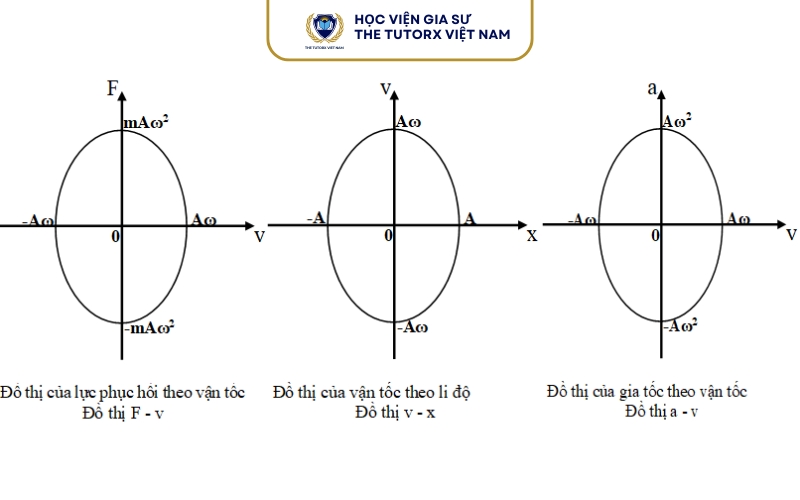
Bảng so sánh nhanh:
| Đại lượng | Tại vị trí cân bằng | Tại vị trí biên |
|---|---|---|
| Li độ (x) | 0 | ±A |
| Vận tốc (v) | Cực đại | 0 |
| Gia tốc (a) | 0 | Cực đại |
Đồ thị gia tốc trong dao động điều hòa
Đồ thị gia tốc là một phần quan trọng trong các bài tập nhận dạng và phân tích dao động điều hòa.
Dạng đồ thị gia tốc – thời gian
- Đồ thị là đường hình sin hoặc cos
- Chu kỳ đồ thị gia tốc bằng chu kỳ dao động
- Biên độ đồ thị gia tốc là amax = ω²A
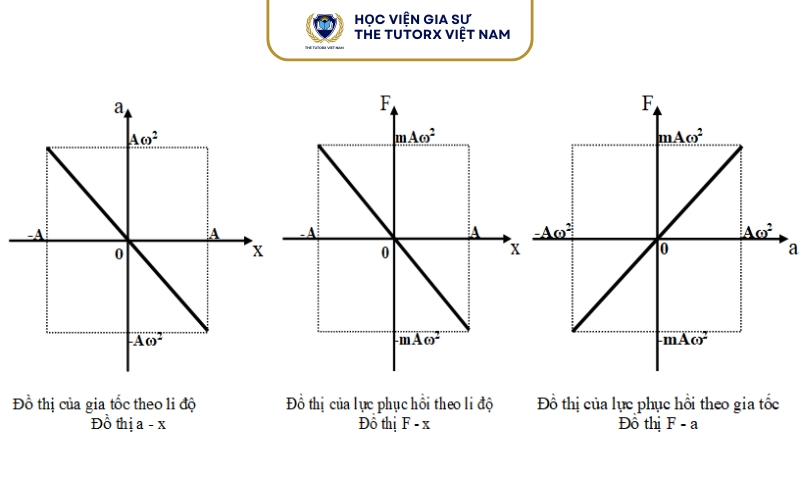
So sánh đồ thị gia tốc với li độ
- Đồ thị gia tốc ngược pha với đồ thị li độ
- Khi đồ thị li độ đạt cực đại ⇒ đồ thị gia tốc đạt cực tiểu
Nếu đồ thị ngược chiều với li độ, rất có thể đó là đồ thị gia tốc dao động điều hòa.
Xem thêm: Dịch vụ gia sư Lý lớp 11 chất lượng
Các dạng bài tập về gia tốc dao động điều hòa
Phần bài tập giúp củng cố kiến thức và là nội dung thường xuyên xuất hiện trong đề kiểm tra, thi THPT.
Dạng 1: Tính gia tốc tại một thời điểm xác định
Phương pháp:
Viết phương trình li độ x(t)
Thay vào công thức a = –ω²x
Ví dụ:
Vật dao động với ω = 10 rad/s, tại thời điểm t có x = 2 cm
→ a = –(10)² × 0,02 = –2 m/s²
Dạng 2: Tính gia tốc cực đại
Công thức áp dụng:
amax = ω²A
Ví dụ:
Biên độ A = 5 cm, ω = 20 rad/s
→ amax = 20² × 0,05 = 20 m/s²
Dạng 3: So sánh gia tốc tại các vị trí khác nhau
Nguyên tắc:
- |x| càng lớn ⇒ |a| càng lớn
- Gia tốc lớn nhất tại biên
- Gia tốc bằng 0 tại vị trí cân bằng
Dạng 4: Bài tập đồ thị gia tốc
Cách làm:
- Xác định biên độ đồ thị ⇒ suy ra ω²A
- Dựa vào chu kỳ đồ thị ⇒ xác định ω
- So sánh pha giữa gia tốc – li độ – vận tốc
Gia tốc dao động điều hòa là đại lượng thể hiện rõ bản chất lực kéo vật về vị trí cân bằng. Việc nắm chắc công thức a = –ω²x, hiểu mối quan hệ giữa gia tốc – vận tốc – li độ và thành thạo các dạng bài tập sẽ giúp bạn dễ dàng chinh phục các câu hỏi về dao động điều hòa trong chương trình Vật lý.






















![[THỨ BẢY HÀNG TUẦN] THE TUTORX WORKSHOP: VẼ TRANH CANVAS - GAM MÀU HẠNH PHÚC](https://thetutorx.vn/thumbs/110x90/2024/website-workshop/website-workshop-1/thumb-workshop-ve-tranh-2.png)


