Nắm rõ công thức tính diện tích tam giác giúp giải Toán nhanh và chính xác. Nếu chưa nhớ, hãy tham khảo bài viết để ôn lại đầy đủ các công thức quan trọng.
Các Dạng Tam Giác Trong Toán Học
Trước khi đi vào công thức, bạn cần phân biệt rõ các loại tam giác:
| Loại tam giác | Đặc điểm |
| Tam giác thường | Không có cạnh hoặc góc nào đặc biệt |
| Tam giác vuông | Có 1 góc vuông (90 độ) |
| Tam giác cân | Có 2 cạnh bên bằng nhau |
| Tam giác đều | Cả 3 cạnh và 3 góc bằng nhau |
| Tam giác vuông cân | Có 1 góc vuông và 2 cạnh góc vuông bằng nhau |
Xác định đúng loại tam giác là bước đầu quan trọng để lựa chọn công thức tính diện tích một cách nhanh chóng và chính xác hơn.
Công Thức Tính Diện Tích Tam Giác Theo Từng Dạng
Công thức tính diện tích tam giác không những có một mà nhiều nhanh giúp giải trở nên dễ dàng hơn. Dưới đây là tổng hợp đầy đủ để người học có thể áp dụng linh hoạt.
Tam Giác Thường
Tùy theo dữ liệu đề bài, bạn có thể áp dụng một trong hai công thức dưới đây:
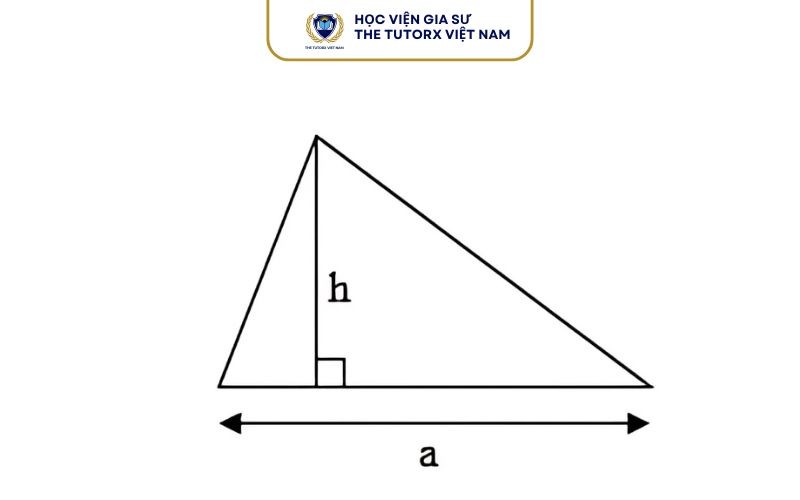
1. Công thức cơ bản (khi biết cạnh đáy và chiều cao)
S = ½ × a × h
Trong đó:
- a: độ dài cạnh đáy
- h: chiều cao tương ứng từ đỉnh đến đáy
Ví dụ: Cho tam giác có đáy a = 6cm, chiều cao h = 4cm. Khi đó:
S = ½ × 6 × 4 = 12cm²
2. Công thức Heron (khi biết đủ ba cạnh a, b, c)
S = √p(p – a)(p – b)(p – c)
Trong đó:
- p (nửa chu vi) = (a + b + c) ÷ 2
Ví dụ: Tính diện tích tam giác có các cạnh 5 cm, 6 cm, 7 cm.
Ta có: p = (5 + 6 + 7) ÷ 2 = 9
⇒ S = √9(9 – 5)(9 – 6)(9 – 7) = 14.7cm²
Tam Giác Cân
Công thức tính diện tích tam giác cân tương tự như tam giác thường:
S = ½ × a × h
Ví dụ: Cho tam giác cân có cạnh đáy a = 8cm, chiều cao từ đỉnh xuống đáy h = 5cm.
Khi đó: S = ½ × 8 × 5 = 20cm²
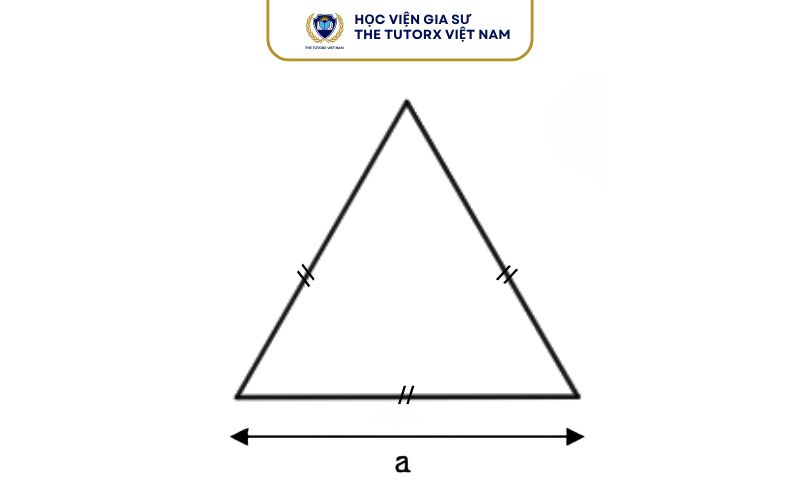
Tam Giác Đều
Vì tam giác đều có 3 cạnh bằng nhau và góc nào cũng 60 độ, ta dùng công thức riêng:
S = (a² × √3) ÷ 4
Trong đó a là độ dài một cạnh của tam giác
Ví dụ: Tính diện tích tam giác đều cạnh a = 6cm:
S = (6² × √3) ÷ 4 = 9√3cm²
Tam Giác Vuông
trong tam giác vuông thì hai cạnh góc vuông làm đáy và chiều cao. Giả sử là a và b:
S = ½ × a × b
Ví dụ: Tam giác vuông có cạnh góc vuông dài 3 cm và 4 cm thì:
S = ½ × 3 × 4 = 6cm²
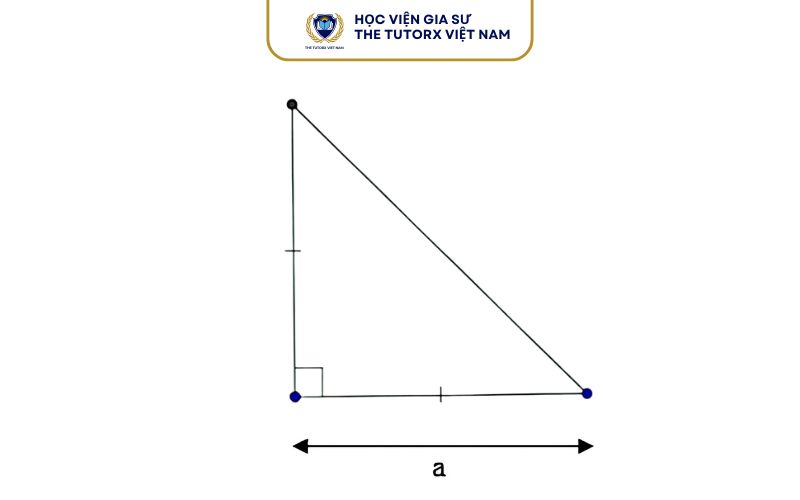
Tam Giác Vuông Cân
Đây là dạng đặc biệt của tam giác vuông. Gọi a là cạnh góc vuông:
S = a² ÷ 2
Trong đó a là độ dài cạnh góc vuông.
Ví dụ: Tính diện tích tam giác vuông cân có cạnh góc vuông dài 5 cm:
S = 5² ÷ 2 = 12.5 cm²
Công thức tính diện tích tam giác là kiến thức nền tảng được giảng dạy từ lớp 5. Nếu con bạn đang gặp khó khăn trong việc ghi nhớ công thức, hiểu bài hay áp dụng vào bài tập thực tế, hãy để The TutorX hỗ trợ.
Chúng tôi cung cấp dịch vụ gia sư lớp 5 uy tín, chuyên dạy kèm môn Toán tại nhà hoặc online với lịch học linh hoạt. Mỗi học sinh đều được thiết kế giáo án cá nhân hóa phù hợp với năng lực và mục tiêu học tập, giúp các em củng cố kiến thức, nâng cao tư duy và thành thạo kỹ năng giải Toán nhanh, chính xác.
Bài viết trên đã hệ thống lại toàn diện các công thức tính diện tích tam giác. Nếu còn bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với The TutorX để được hỗ trợ kịp thời.


















![[THỨ BẢY HÀNG TUẦN] THE TUTORX WORKSHOP: VẼ TRANH CANVAS - GAM MÀU HẠNH PHÚC](https://thetutorx.vn/thumbs/110x90/2024/website-workshop/website-workshop-1/thumb-workshop-ve-tranh-2.png)


