Công Thức Tính Diện Tích Hình Tứ Diện Chuẩn Xác

Tính diện tích hình tứ diện là kiến thức quan trọng trong hình học không gian. Bài viết này Gia Sư Giỏi The TutorX sẽ hướng dẫn bạn công thức chuẩn xác và các ví dụ minh họa, giúp bạn áp dụng dễ dàng trong học tập và giải bài toán thực tế.

Hình tứ diện là gì?

Hình tứ diện là một trong những hình học không gian cơ bản, được tạo thành từ bốn mặt tam giác và bốn đỉnh. Mỗi mặt của tứ diện đều là tam giác, và bất kỳ ba đỉnh nào cũng không nằm trên cùng một đường thẳng. Trong hình học, tứ diện là dạng hình học đơn giản nhất trong không gian 3 chiều.

Có hai loại tứ diện phổ biến:

• Tứ diện đều: tất cả các cạnh bằng nhau, tất cả các mặt là tam giác đều.
• Tứ diện bất kỳ: các cạnh và mặt không nhất thiết bằng nhau.

Tứ diện xuất hiện trong nhiều bài toán hình học, vật lý và cả trong đời sống thực tế, ví dụ như trong cấu trúc tinh thể của một số khoáng vật.

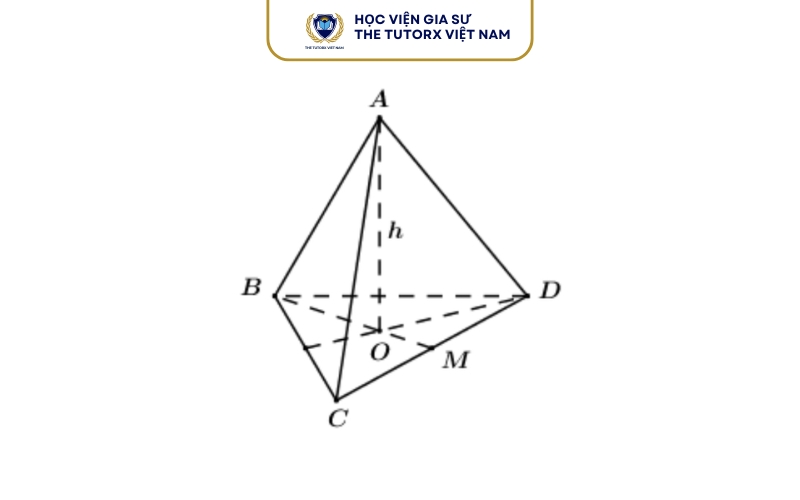
Tính chất của hình tứ diện

Hiểu rõ tính chất của tứ diện sẽ giúp bạn áp dụng công thức diện tích hình tứ diện chính xác hơn. Một số tính chất cơ bản gồm:

• Mỗi mặt là tam giác: tứ diện có tổng cộng 4 mặt.
• Có 4 đỉnh và 6 cạnh: mỗi đỉnh nối với 3 đỉnh còn lại.
• Tâm trọng tứ diện: giao điểm của các đường trung tuyến (đường nối đỉnh với trung điểm mặt đối diện) là trọng tâm, chia tỷ lệ 3:1.
• Tứ diện đều: tất cả các cạnh bằng nhau và tất cả các góc mặt bằng nhau.

Nhờ những tính chất này, bạn có thể dễ dàng tính diện tích và thể tích tứ diện khi biết các thông số cần thiết.

Công thức Diện tích hình tứ diện

Có nhiều cách để tính diện tích hình tứ diện, tùy vào loại tứ diện và thông số đã biết:

Diện tích tứ diện đều

Nếu tứ diện là đều và có cạnh bằng a, diện tích toàn phần được tính bằng:

S = √3 x a²

Trong đó, S là diện tích toàn phần của tứ diện đều, a là độ dài mỗi cạnh.

Diện tích tứ diện bất kỳ theo các mặt tam giác

Nếu bạn biết diện tích từng mặt tam giác, tổng diện tích hình tứ diện là:

S= S₁+S₂+S₃+S₄

Trong đó: S₁,S₂,S₃,S₄ là diện tích các mặt tam giác

Diện tích tứ diện theo công thức Heron 3D

Với tam giác có ba cạnh a,b,c, diện tích từng mặt có thể tính bằng công thức Heron:

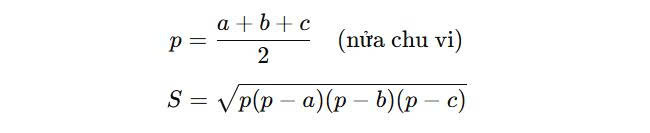
Áp dụng công thức này cho mỗi mặt, sau đó cộng lại sẽ ra diện tích hình tứ diện bất kỳ.

Xem thêm: Dịch vụ Gia sư toán lớp 11 chất lượng

Một số dạng bài tập cơ bản về hình tứ diện

Bài tập 1: Tính diện tích tứ diện đều 

Đề bài: Cho tứ diện đều có cạnh a=4 cm. Tính diện tích tứ diện.
Giải: Áp dụng công thức:

S = √3 x a² =√3 x 4² = 16√3 cm²

Bài tập 2: Tính diện tích tứ diện theo diện tích mặt tam giác

Đề bài: Tứ diện có các mặt tam giác có diện tích lần lượt là 6, 7, 8, 9 cm². Tính diện tích tứ diện.
Giải: Tổng diện tích các mặt:

S=6+7+8+9=30cm²

Bài tập 3: Tính diện tích tứ diện bất kỳ theo Heron

Đề bài: Một mặt tam giác của tứ diện có ba cạnh 3 cm, 4 cm, 5 cm. Tính diện tích mặt đó.

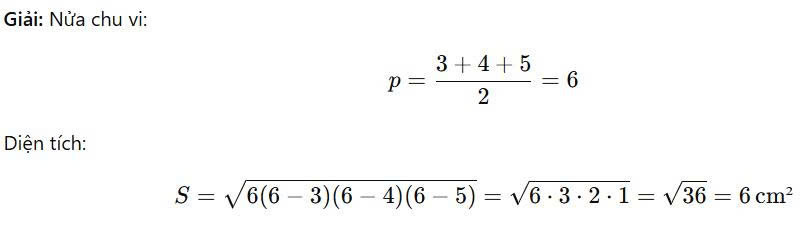
Hiểu rõ và áp dụng đúng công thức tính diện tích hình tứ diện giúp việc giải các bài toán về tứ diện trở nên nhanh chóng và chính xác. Dù là tứ diện đều hay bất kỳ tứ diện nào, việc nắm vững các tính chất và công thức cơ bản sẽ hỗ trợ bạn tính diện tích một cách dễ dàng. Hãy luyện tập thêm các bài tập minh họa để củng cố kiến thức và tự tin áp dụng trong học tập cũng như các bài toán thực tế.