Y CosX Đồng Biến Trên Khoảng Nào? Lý Thuyết Và Cách Xác Định Chi Tiết

Trong chương trình Toán học phổ thông, đặc biệt là giải tích lớp 11, câu hỏi “y cosx đồng biến trên khoảng nào?” là dạng bài rất quen thuộc. Để trả lời chính xác, học sinh cần nắm được điều kiện đồng biến, đạo hàm của hàm số y = cos x và dấu của đạo hàm trên từng khoảng. Bài viết dưới đây trung tâm gia sư The TutorX sẽ giúp bạn hiểu bản chất vấn đề và ghi nhớ cách làm nhanh – đúng – dễ áp dụng khi làm bài tập và thi cử.

Điều kiện để hàm cos x đồng biến

Theo định nghĩa, một hàm số y=f(x) được gọi là đồng biến trên một khoảng nếu:

• Đạo hàm f′(x)≥0 với mọi x thuộc khoảng đó
• Và f′(x)>0 tại nhiều điểm trong khoảng

Như vậy, để xét y = cos x đồng biến trên khoảng nào, ta cần:

• Tính đạo hàm của hàm số y = cos x
• Xét dấu của đạo hàm
• Tìm các khoảng mà đạo hàm không âm

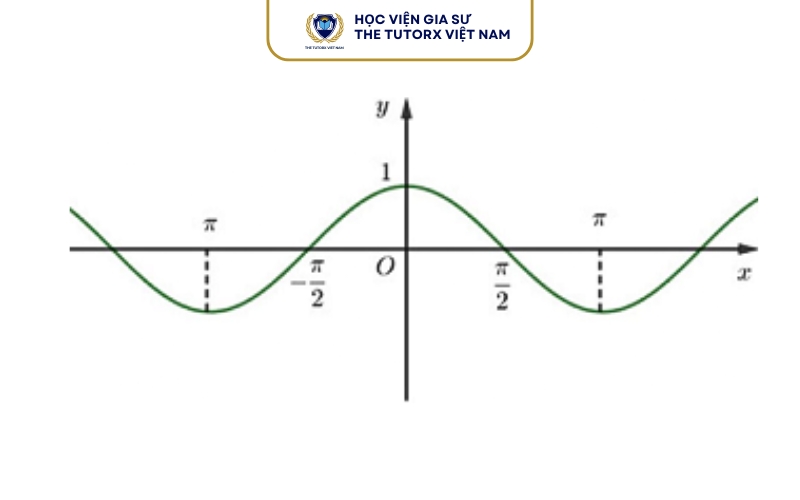
Đạo hàm của hàm số y = cos x

Xét hàm số:

y=cosx

Đạo hàm của hàm số là:

y′=−sinx

Từ đây có thể thấy, tính đồng biến của hàm cos x phụ thuộc trực tiếp vào dấu của sin x.

>>> Xem thêm: Dịch vụ gia sư toán lớp 11 dạy kèm tại nhà

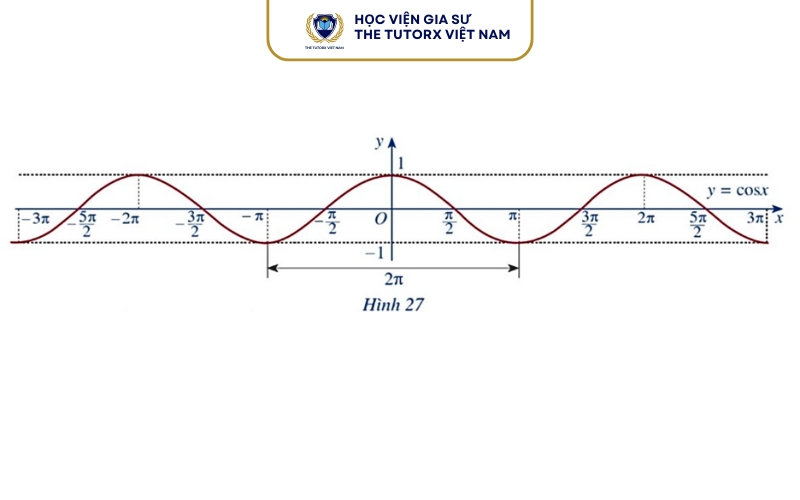
Y cosx đồng biến trên khoảng nào?

Ta có:

y′ =−sinx

Hàm số y = cos x đồng biến khi:

y′≥0⟺−sinx≥0⟺sinx≤0

Xét dấu của sin x

Hàm số sinx≤0 trên các khoảng:

[kπ,(k+1)π],k∈Z

Hàm số y = cos x đồng biến trên các khoảng:

[kπ,(k+1)π],k∈Z

Nói cách khác, cứ mỗi chu kỳ π, hàm cos x sẽ có một khoảng đồng biến liên tiếp.

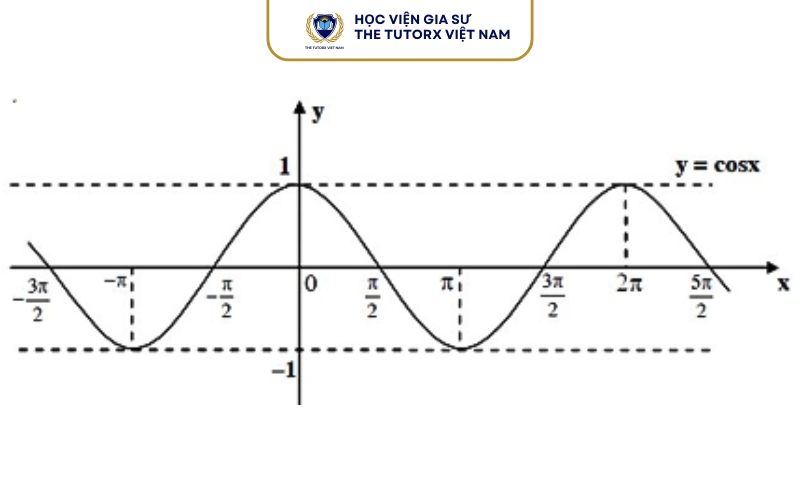
Ví dụ minh họa:

y = cos x đồng biến trên:

[0,π]

[π,2π]

[−π,0]

Qua bài viết, có thể thấy rằng việc xác định y cosx đồng biến trên khoảng nào không hề phức tạp nếu bạn nắm vững mối liên hệ giữa đạo hàm và dấu của hàm lượng giác. Chỉ cần nhớ đạo hàm của 
y=cosx là y'=−sinx, từ đó suy ra hàm số cos x đồng biến khi sinx≤0, tức trên các khoảng [kπ,(k+1)π] với k∈Z. Đây là kiến thức nền tảng, thường xuyên xuất hiện trong bài tập và đề thi, vì vậy việc hiểu rõ bản chất và ghi nhớ quy tắc sẽ giúp bạn làm bài nhanh, chính xác và tránh nhầm lẫn không đáng có.

>>> Xem thêm: Top các trung tâm gia sư uy tín tại TPHCM dạy kèm tại nhà